Как се изчислява възвръщаемост на инвестициите (ROI)

В основата на всяка инвестиция стои предположението за постигане на определена възвръщаемост. Това представлява желанието на човек да намали стандарта си на живот в настоящето, като спестява пари, за да ги насочи към бъдещи финансови печалби.

Но какви методи трябва да използваме, за да изчислим нашите печалби или загуби? Как да отчитаме активно управлявани инвестиционни портфейли, в които фондове се вливат и изтеглят? Какви показатели за възвръщаемост се използват за сравняване на представянето на портфейли?

В тази статия ще разгледам най-често използваните методи за изчисляване на възвръщаемостта на инвестициите в различни обстоятелства. 

Бих искал обаче да подчертая, че за повечето инвеститори първите три метода са напълно достатъчни. Разделът с напредналите методи е за тези, които искат по-задълбочено разбиране за развитието на техния инвестиционен портфейл.

Проста възвръщаемост

Най-основният начин за изчисляване на очаквана доходност или загуба от инвестиция е чрез формулата за проста възвръщаемост. Тя се представя под формата на процент. Този процент показва колко е спечелил или загубил човек от инвестицията.

Формулата за проста възвръщаемост е:

Тази формула е валидна само за краткосрочни инвестиции, които не отчитат допълнителни инвестиции или ликвидация (продажба на активи) по време на инвестиционния период. Освен това тази формула не взема предвид всички видове такси и комисиони, платени на търговската платформа.

Годишна възвръщаемост

Годишната възвръщаемост помага да се определи каква е годишната възвръщаемост на инвестиция за период от няколко години. 

Каква е разликата в сравнение с простата възвръщаемост? Фактът, че възвръщаемостта на инвестициите е компаундната. Това означава, че възвръщаемостта за следващата година ще се добави към вече съществуващата възвръщаемост за тази година. Тази година възвръщаемостта се натрупва върху възвръщаемостта от миналата година и така нататък.

Тъй като сумите се увеличават експоненциално през по-дълги периоди от време в сравнение с простата възвръщаемост, трябва да използваме подходящ начин за изчисляване на годишната възвръщаемост, която се компаундва за инвестиционния период.

За да изчислим математически годишната възвръщаемост на инвестиция, първо трябва да разгледаме формулата за сложна лихва:

Ако знаем крайната сума (след като инвестицията е направена), началната сума (която сме инвестирали) и за колко години (брой периоди N), трябва да изчислим лихвения процент, който представлява годишната възвръщаемост. 

Извеждайки лихвения процент, получаваме:

С течение на времето диверсифицираните портфейли се възползват от годишна възвръщаемост между 8% и 12%. Недостатъкът на тази формула, както и в случая с простата възвръщаемост, е фактът, че тя не отчита потоците от пари към и извън инвестиционния портфейл.

Обща възвръщаемост

Двата предишни показателя за изчисляване на възвръщаемостта на инвестициите са предназначени да изразят възвръщаемостта от увеличение на цените. Въпреки това тези възвръщаемости не отчитат допълнителните печалби от инвестицията.

Тук става дума за дивиденти от акции. Това също са приходи, генерирани от същата инвестиция, и те също трябва да бъдат отчетени. Разликата между увеличението на цените и общата възвръщаемост на S&P500 показва голямата разлика, която дивидентите могат да направят.

За да отчетем и дивидентите, трябва да използваме следната формула:

Формулата е почти идентична с тази за простата възвръщаемост, но именно защото тази формула има за цел да покаже финансовата печалба за целия инвестиционен период. Въпреки това, дори общата възвръщаемост не отчита паричните потоци по време на инвестиционния период.

Нетна настояща стойност (NPV)

Трите формули, споменати по-горе, са полезни за изчисляване на възвръщаемостта на инвестицията (ROI), след като инвестицията вече е направена. Но какво ще стане, ако искаме да изчислим за колко време инвестицията ни ще започне да носи печалба?

С други думи, кога можем да очакваме да спечелим повече, отколкото сме инвестирали? За да разберем това, трябва да изчислим нетната настояща стойност (NPV) на потенциалната инвестиция.

Всички сме чували, че едно евро днес струва повече от едно евро утре. Това се дължи както на инфлацията, така и на предпочитанията на хората за настоящето. Хората обикновено искат нещата сега, защото настоящето е по-сигурно от една година в бъдеще. Това е и една от причините много от нас да решават да вземат заем, за да купят кола или къща.

Повече по темата тук: Какво са парите?

Същата концепция се прилага и за инвестициите. В бизнеса стойността на инвестицията на една компания зависи от това колко и колко бързо тази инвестиция може да генерира парични потоци. За да изчислим настоящата (или текущата) стойност на парите, които ще получим в бъдеще, трябва да разгледаме тези приходи в настоящето.

Правим това, като дисконтираме бъдещите парични потоци спрямо разходите за реализиране на този проект. Тези разходи се представят като годишен процент, който е претеглената средна стойност на цената на акционерния капитал и дълга, използвани за тази инвестиция.

Формулата изглежда така:

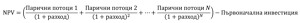
N е броят на годините. Това помага да се определи каква е стойността днес на парите, които ще получим в бъдеще. Тези парични потоци трябва да бъдат по-големи от началната инвестиция за периода на инвестицията, за да се гарантира, че инвестицията си струва повече от вложената сума.

Ако NPV е отрицателна, това означава, че имаме реална загуба и трябва да пренасочим средствата към проекти с по-висока възвръщаемост. NPV ни показва в какво не трябва да инвестираме.

Методи за изчисляване на възвръщаемостта на инвестициите за напреднали

За някой, който просто иска бързо да разбере колко печалба е направил от инвестиция, горепосочените формули са напълно достатъчни. Въпреки това за по-напредналите инвеститори съществуват и други формули, които могат да бъдат използвани.

Ще изброя четири от тях по-долу и ще обясня какви са техните предимства. Това зависи основно от интереса на инвеститора към това, което той или тя иска да открие.

Вътрешната норма на възвръщаемост (IRR)

Вътрешната норма на възвръщаемост е тясно свързана с нетната настояща стойност (NPV). Формулата ѝ е изведена от NPV. 

IRR оценява колко бързо инвеститор може да възвърне своята инвестиция, като взема предвид времевата стойност на парите. Тя се изразява като средна годишна норма на възвръщаемост.

За да намерим IRR, трябва да приравним формулата на NPV на нула. 

Така формулата би изглеждала така:

Както можете да видите, „разходът“ в знаменателя е заменен с IRR. Чрез решаване на това уравнение можем да открием максималната годишна възвръщаемост на инвестицията. Въпреки това, IRR може да бъде изчислен и с помощта на електронна таблица (Excel или Google Sheets), като се въведе формулата „=IRR“ и се попълнят скобите с правилните данни.

В повечето случаи IRR се използва като метод за прогнозиране на инвестиционни решения. То също може да помогне за оценка на възвръщаемостта на вложения капитал в различни инвестиции, направени на точни времеви интервали.

Все пак IRR има две основни ограничения. Първо, инвестициите трябва да бъдат направени на точни времеви интервали. Второ, може да има само положителни парични потоци, което означава, че повече не влагаме средства в тази инвестиция.

Парично претеглена норма на възвръщаемост (MWRR или XIRR)

За да коригираме проблема с честотата на инвестициите, парично претеглената норма на възвръщаемост отчита паричните потоци и в двете посоки. Така че, ако сте активен инвеститор, най-вероятно ще използвате този показател, за да разберете годишната възвръщаемост на портфейла си.

MWRR показва възвръщаемостта на портфейла, като взема предвид момента, в който инвеститорът е вложил или изтеглил средства от портфейла. Този индикатор може да бъде много полезен за показване на това колко голямо влияние може да окаже неправилният момент на пазара.

За да изчислите MWRR, е по-лесно да използвате електронна таблица (отново Excel или Google Sheets). Формулата, която трябва да се използва, е „=XIRR“, последвана от данните за паричните потоци и конкретните дати.

Времево претеглена норма на възвръщаемост (TWRR)

Ако MWRR показва колко добър предсказател е инвеститорът, TWRR се фокусира изцяло върху представянето на портфейла, без да отчита паричните потоци. Този индикатор се използва най-често за сравняване на представянето на портфейли от управляващи фондове и ETF.

За да изчислим TWRR, ще разгледам един прост пример, за да направя стъпките лесни за разбиране. 

Да предположим, че някой е купил една акция от SPY ETF, който следи S&P500 и се управлява от State Street, на 3 януари 2023 г. на цена от 380 долара. На 27 юли индексът достига върхова стойност от 455 долара/акция, така че инвеститорът купува още една акция. Каква е възвръщаемостта на инвеститора между 1 януари и 29 декември 2023 г., ако на 29 декември една акция SPY струва 475 долара?

Първо, трябва да определим нашите времеви периоди. 

Следователно имаме:

• 3 януари – 27 юли
• 27 юли – 29 декември

Сега трябва да изчислим простите възвръщаемости за всеки от тези периоди.

Сега, когато имаме възвръщаемостите, трябва да изчислим цялостната възвръщаемост на портфейла за 2023 година. Това се прави чрез геометрично свързване на възвръщаемостите. 

Формулата е следната:

След като извършим изчисленията, TWRR е равно на 25%. Но какво всъщност изчислихме? Ако изчислим простата възвращаемост на цената на акцията, получаваме точно 25%. Следователно, както беше посочено по-горе, TWRR помага да се изчисли единствено представянето на портфейла, без да се отчитат паричните потоци.

За сравнение, MWRR в този пример е 7,78%. Тъй като е по-ниска от възвращаемостта на самия портфейл, това показва, че инвеститорът не е взел най-доброто решение, като е инвестирал на пазарен връх.

Коефициент на Шарп

Последният метод за изчисляване на възвръщаемостта от нашия списък е коефициентът на Шарп. Той показва възвръщаемостта на инвестицията спрямо риска, който носи. Това може да бъде много полезен индикатор при претегляне на риска и възвръщаемостта при сравняване на инвестиционни портфейли.

Рискът е волатилността на портфейла. Това измерва колко се отклонява стойността на портфейла от средната цена. Това може да бъде изчислено чрез формулата „=STDEV“ в електронна таблица. 

След като получим тази стойност, трябва да изчислим простата възвращаемост на инвестицията и да извадим безрисковия процент. Безрисковият процент обикновено е доходността на краткосрочни държавни облигации. Нека разгледаме пример.

Индексът S&P500 имаше проста възвръщаемост от 24,22% през 2023 г. Волатилността на индекса, използвайки Excel, показва отклонение от 39,17%. Доходността на едногодишната облигация на правителството на САЩ беше около 5%. 

Коефициентът на Шарп е:

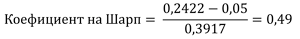
Този коефициент от 0,49 показва слабо представяне на индекса S&P500 спрямо неговата волатилност през 2023 година. В повечето случаи коефициент на Шарп над 1 се счита за добро инвестиционно решение.

Заключение

Бих искал да поздравя всички, които преминаха през статията дотук. Започнахме с лесни методи за изчисляване на печалбите и загубите и завършихме с възвръщаемост, отчитаща риска и времевата стойност на парите.

Искам да подчертая, че почти никой обикновен инвеститор няма нужда от тези формули. Търговските платформи вече имат вградени начини за показване на възвръщаемостта на инвеститора, отчитайки паричните потоци. 

Идеално е нещата да се опростяват, иначе целият процес на инвестиране може да изплаши хората. А това е крайно нежелателно, защото само чрез инвестиране в активи можем да увеличим богатството си.